Parameter Study with discrete parameter¶
This example is identical to Parameter Study, but in this case par4 is a discrete parameter.
%matplotlib inline
import sys,os
try:
import matk
except:
try:
sys.path.append(os.path.join('..','src'))
import matk
except ImportError as err:
print 'Unable to load MATK module: '+str(err)
import numpy
from scipy import arange, randn, exp
from multiprocessing import freeze_support
# Model function
def dbexpl(p):
t=arange(0,100,20.)
y = (p['par1']*exp(-p['par2']*t) + p['par3']*exp(-p['par4']*t))
return y
# Setup MATK model with parameters
p = matk.matk(model=dbexpl)
p.add_par('par1',min=0,max=1)
p.add_par('par2',min=0,max=0.2)
p.add_par('par3',min=0,max=1)
# Create discrete parameter with 21 bins and uniform probabilities
vals = numpy.linspace(0,0.2,21)
probs = [1./20.]*21
p.add_par('par4',discrete_vals = (vals,probs))
# Create full factorial parameter study with 3 values for each parameter
s = p.parstudy(nvals=[3,3,3,3])
# Print values to make sure you got what you wanted
print "\nParameter values:"
print s.samples.values
Parameter values:
[[ 0. 0. 0. 0. ]
[ 0. 0. 0. 0.1]
[ 0. 0. 0. 0.2]
[ 0. 0. 0.5 0. ]
[ 0. 0. 0.5 0.1]
[ 0. 0. 0.5 0.2]
[ 0. 0. 1. 0. ]
[ 0. 0. 1. 0.1]
[ 0. 0. 1. 0.2]
[ 0. 0.1 0. 0. ]
[ 0. 0.1 0. 0.1]
[ 0. 0.1 0. 0.2]
[ 0. 0.1 0.5 0. ]
[ 0. 0.1 0.5 0.1]
[ 0. 0.1 0.5 0.2]
[ 0. 0.1 1. 0. ]
[ 0. 0.1 1. 0.1]
[ 0. 0.1 1. 0.2]
[ 0. 0.2 0. 0. ]
[ 0. 0.2 0. 0.1]
[ 0. 0.2 0. 0.2]
[ 0. 0.2 0.5 0. ]
[ 0. 0.2 0.5 0.1]
[ 0. 0.2 0.5 0.2]
[ 0. 0.2 1. 0. ]
[ 0. 0.2 1. 0.1]
[ 0. 0.2 1. 0.2]
[ 0.5 0. 0. 0. ]
[ 0.5 0. 0. 0.1]
[ 0.5 0. 0. 0.2]
[ 0.5 0. 0.5 0. ]
[ 0.5 0. 0.5 0.1]
[ 0.5 0. 0.5 0.2]
[ 0.5 0. 1. 0. ]
[ 0.5 0. 1. 0.1]
[ 0.5 0. 1. 0.2]
[ 0.5 0.1 0. 0. ]
[ 0.5 0.1 0. 0.1]
[ 0.5 0.1 0. 0.2]
[ 0.5 0.1 0.5 0. ]
[ 0.5 0.1 0.5 0.1]
[ 0.5 0.1 0.5 0.2]
[ 0.5 0.1 1. 0. ]
[ 0.5 0.1 1. 0.1]
[ 0.5 0.1 1. 0.2]
[ 0.5 0.2 0. 0. ]
[ 0.5 0.2 0. 0.1]
[ 0.5 0.2 0. 0.2]
[ 0.5 0.2 0.5 0. ]
[ 0.5 0.2 0.5 0.1]
[ 0.5 0.2 0.5 0.2]
[ 0.5 0.2 1. 0. ]
[ 0.5 0.2 1. 0.1]
[ 0.5 0.2 1. 0.2]
[ 1. 0. 0. 0. ]
[ 1. 0. 0. 0.1]
[ 1. 0. 0. 0.2]
[ 1. 0. 0.5 0. ]
[ 1. 0. 0.5 0.1]
[ 1. 0. 0.5 0.2]
[ 1. 0. 1. 0. ]
[ 1. 0. 1. 0.1]
[ 1. 0. 1. 0.2]
[ 1. 0.1 0. 0. ]
[ 1. 0.1 0. 0.1]
[ 1. 0.1 0. 0.2]
[ 1. 0.1 0.5 0. ]
[ 1. 0.1 0.5 0.1]
[ 1. 0.1 0.5 0.2]
[ 1. 0.1 1. 0. ]
[ 1. 0.1 1. 0.1]
[ 1. 0.1 1. 0.2]
[ 1. 0.2 0. 0. ]
[ 1. 0.2 0. 0.1]
[ 1. 0.2 0. 0.2]
[ 1. 0.2 0.5 0. ]
[ 1. 0.2 0.5 0.1]
[ 1. 0.2 0.5 0.2]
[ 1. 0.2 1. 0. ]
[ 1. 0.2 1. 0.1]
[ 1. 0.2 1. 0.2]]
# Look at sample parameter histograms
out = s.samples.hist(ncols=2,title='Parameter Histograms by Counts')
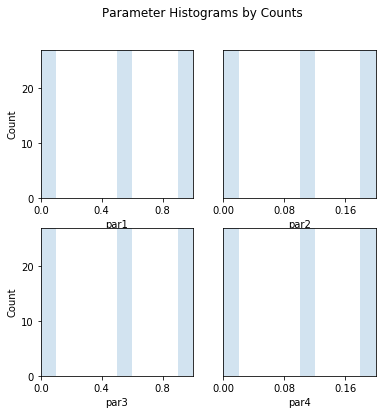
par1:
Count: 27 0 0 0 0 27 0 0 0 27
Bins: 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
par2:
Count: 27 0 0 0 0 27 0 0 0 27
Bins: 0 0.02 0.04 0.06 0.08 0.1 0.12 0.14 0.16 0.18 0.2
par3:
Count: 27 0 0 0 0 27 0 0 0 27
Bins: 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
par4:
Count: 27 0 0 0 0 27 0 0 0 27
Bins: 0 0.02 0.04 0.06 0.08 0.1 0.12 0.14 0.16 0.18 0.2
# This time use frequency instead of count and turn off printing histogram to screen
out = s.samples.hist(ncols=2,title='Parameter Histograms by Frequency',frequency=True,printout=False)
# Run model with parameter samples
s.run( cpus=2, outfile='results.dat', logfile='log.dat',verbose=False)
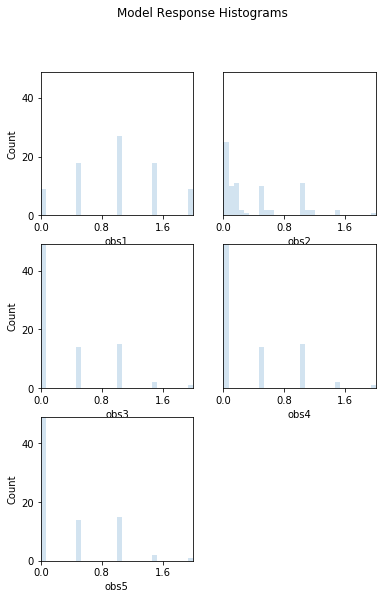
# Look at response histograms, correlations, and panels
# Note that printout has been set to False in this case to avoid printing histogram output to screen
out = s.responses.hist(ncols=2, bins=30, title='Model Response Histograms',printout=False)
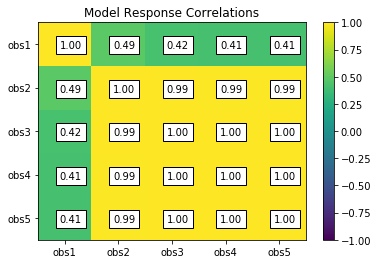
rescor = s.responses.corr(plot=True, title='Model Response Correlations',printout=False)
s.responses.panels(title='Response Panels')
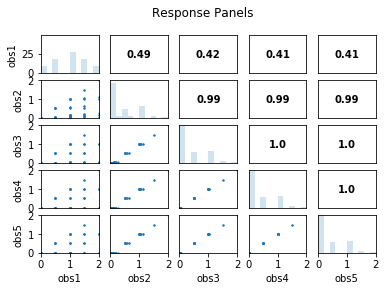
# Print and plot parameter/response correlations
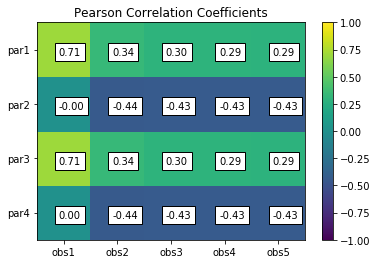
print "\nPearson Correlation Coefficients:"
pcorr = s.corr(plot=True,title='Pearson Correlation Coefficients')
Pearson Correlation Coefficients:
obs1 obs2 obs3 obs4 obs5
par1 0.71 0.34 0.30 0.29 0.29
par2 -0.00 -0.44 -0.43 -0.43 -0.43
par3 0.71 0.34 0.30 0.29 0.29
par4 0.00 -0.44 -0.43 -0.43 -0.43
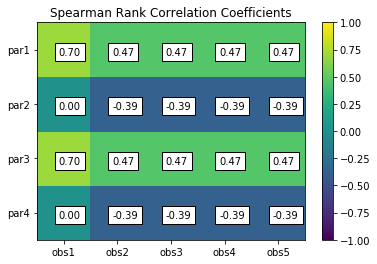
scorr = s.corr(plot=True,type='spearman',title='Spearman Rank Correlation Coefficients',printout=False)
s.panels(figsize=(10,8))
