Subsetting samples based on model output¶
This example demonstrates a case where a sample is subsetted based on model output.
This example builds on the Sampling example.
Failed model calls are created by returning nans for some parameter combinations.
These samples are collected from the sampleset using the subset function.
It is then easy to identify in the diagnostic plots where the problem is occurring.
This example demonstrates a Latin Hypercube Sampling of a 4 parameter 5 response model using the lhs function.
The models of the parameter study are run using the run function.
The generation of diagnostic plots is demonstrated using hist, panels, and corr.
# %load sampling_na.py
%matplotlib inline
import sys,os
try:
import matk
except:
try:
sys.path.append(os.path.join('..','src'))
import matk
except ImportError as err:
print 'Unable to load MATK module: '+str(err)
import numpy
from scipy import arange, randn, exp
from multiprocessing import freeze_support
# Model function
def dbexpl(p):
t=arange(0,100,20.)
# Catch error, in this case a simple example
# These could be failed model simulations
if (p['par1']) < 0.5:
#if (p['par1']+p['par3']) < 0.25:
return [numpy.nan]*len(t)
y = (p['par1']*exp(-p['par2']*t) + p['par3']*exp(-p['par4']*t))
return y
# Setup MATK model with parameters
p = matk.matk(model=dbexpl)
p.add_par('par1',min=0,max=1)
p.add_par('par2',min=0,max=0.2)
p.add_par('par3',min=0,max=1)
p.add_par('par4',min=0,max=0.2)
# Create LHS sample
s = p.lhs(siz=500, seed=1000)
# Look at sample parameter histograms, correlations, and panels
out = s.samples.hist(ncols=2,title='Parameter Histograms')
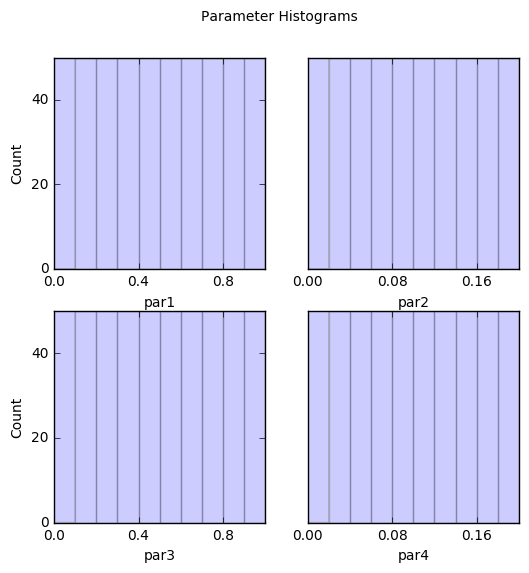
par1:
Count: 50 50 50 50 50 50 50 50 50 50
Bins: 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
par2:
Count: 50 50 50 50 50 50 50 50 50 50
Bins: 0 0.02 0.04 0.06 0.08 0.1 0.12 0.14 0.16 0.18 0.2
par3:
Count: 50 50 50 50 50 50 50 50 50 50
Bins: 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
par4:
Count: 50 50 50 50 50 50 50 50 50 50
Bins: 0 0.02 0.04 0.06 0.08 0.1 0.12 0.14 0.16 0.18 0.2
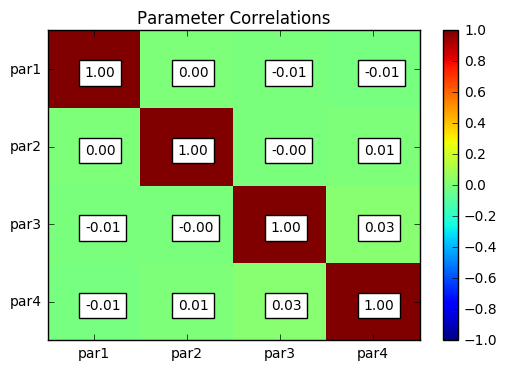
parcor = s.samples.corr(plot=True, title='Parameter Correlations')
par1 par2 par3 par4
par1 1.00 0.00 -0.01 -0.01
par2 0.00 1.00 -0.00 0.01
par3 -0.01 -0.00 1.00 0.03
par4 -0.01 0.01 0.03 1.00
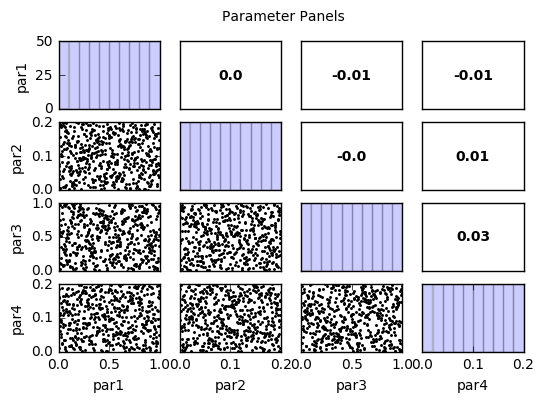
out = s.samples.panels(title='Parameter Panels')
# Run model with parameter samples
s.run( cpus=2, outfile='results.dat', logfile='log.dat',verbose=False)
array([[ 1.20102380e+00, 1.10711918e-01, 1.54519180e-02,
2.43673591e-03, 3.94147491e-04],
[ nan, nan, nan,
nan, nan],
[ nan, nan, nan,
nan, nan],
...,
[ nan, nan, nan,
nan, nan],
[ nan, nan, nan,
nan, nan],
[ 1.25792755e+00, 2.18316358e-01, 4.39592143e-02,
1.00887434e-02, 2.53278272e-03]])
# Look at sample response histograms, correlations, and panels
out = s.responses.hist(ncols=3,title='Model Response Histograms')
Error: Nan values exist probably due to failed simulations. Use subset (e.g. subset([('obs','!=',numpy.nan)]) to remove
# Subset sampleset to only samples with nan responses
snan = s.subset(numpy.isnan, obs='obs1')
# Evaluate parameter combination resulting in nans
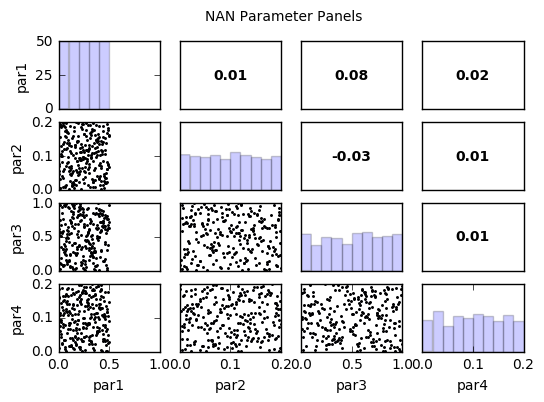
# Note that it is easy to identify that the culprit is par1 with values less than 0.5
out = snan.samples.hist(ncols=2,title='NAN Parameter Histograms')
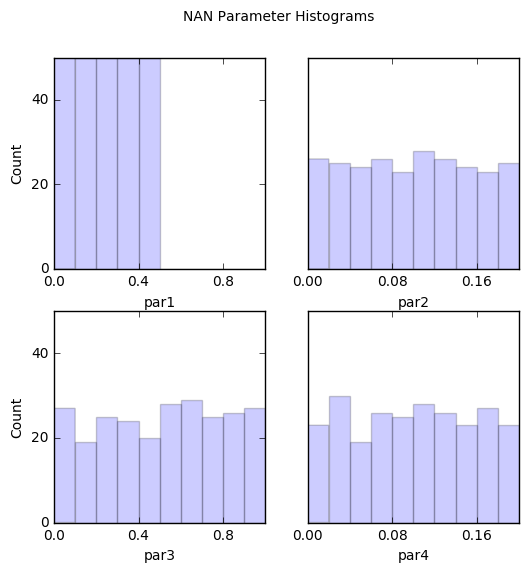
par1:
Count: 50 50 50 50 50 0 0 0 0 0
Bins: 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
par2:
Count: 26 25 24 26 23 28 26 24 23 25
Bins: 0 0.02 0.04 0.06 0.08 0.1 0.12 0.14 0.16 0.18 0.2
par3:
Count: 27 19 25 24 20 28 29 25 26 27
Bins: 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
par4:
Count: 23 30 19 26 25 28 26 23 27 23
Bins: 0 0.02 0.04 0.06 0.08 0.1 0.12 0.14 0.16 0.18 0.2
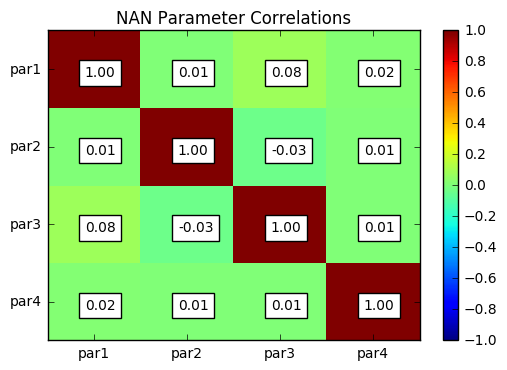
parcor = snan.samples.corr(plot=True, title='NAN Parameter Correlations')
par1 par2 par3 par4
par1 1.00 0.01 0.08 0.02
par2 0.01 1.00 -0.03 0.01
par3 0.08 -0.03 1.00 0.01
par4 0.02 0.01 0.01 1.00
out = snan.samples.panels(title='NAN Parameter Panels')